Many analysts know it: You find a significant correlation - and then you wonder how secure the knowledge actually is. Of course, a good model inevitably requires an evaluation based on test data, because there is no way around it. But sometimes doubts remain - because even test data can be unreliable.
At the beginning of this year, during my work, I found such a significant correlation (0.8 after Spearman). However, an evaluation was only possible to a limited extent, because due to external circumstances many attributes of the data can change in the respective department and not all changes are documented. Incompleteness in the dataset - that too will be known to analysts.
Now I asked myself the question: how can I secure my knowledge nevertheless. The nature of the correlation was of central importance.
The situation was similar to a well-insulated building in which the room temperature is dependent on both the outside temperature and a heating. Due to the thick insulation of the building, the outside temperature has a time delay of about two days. After these two days, the temperature in the building has dropped so low that the heater will switch on and heat up the interior of the building. In this example, it quickly becomes apparent that this control loop applies only in winter. In the summer one has to do with a heating of the interior with the same time delay of two days. In winter, there is the additional problem that the heating eliminates the correlation between outside and inside temperature.
Now imagine that the heating of the building is under-dimensioned, and it can not keep the interior of the building to temperature, so that the correlation between outside and inside temperature is maintained.
And now we find exactly this correlation - but we do not yet know that the heating is too weak. In general, one would doubt the causality of the correlation, since the building is heated. And that was just the sticking point. So how do you protect the knowledge against "random" correlation? There is no general solution to such problems. But especially for this problem, a solution came to my mind.
What I did not know at the beginning of the investigation was the time span between the Delayed Temperature inside and the outside temperature. So I had to link my data with different time intervals. So I connected the data set of the outside temperature over the date with + X days with the data of the interior temperature and determined the correlation. This was laborious and brought me a series of readings that resembled a curve.
The temperature is constantly changing throughout the year - it is the seasonal element in general. With a time lag of 6 months, the outside temperature reaches its maximum or minimum. After reaching its maximum, the temperature gradually drops after June. After reaching their minimum, the temperature gradually rises after December. At 6 months (ie about 180 days), the correlation of the outside temperature with itself would have to be close to -1 because the behavior of the same magnitude reverses. At three months (about 90 days), the correlation would have to be at zero. The same applies to the interior temperature and +2 days more. Conversely, this would also mean that a curve symmetry would have to be present if the time was shifted in the other direction. So this now had to be tested. I now performed the same elaborate data transformation in the other direction and obtained the following curve of correlation measurements.
So the calculated curve about Spearman's correlation coefficient was actually symmetric, and this suggested that it was not a random correlation but a causal one. In a random correlation, it would be extremely unlikely that the result would follow a curve - let alone a symmetric one. The following graphic illustrates what a random correlation would look like.
At the beginning of this year, during my work, I found such a significant correlation (0.8 after Spearman). However, an evaluation was only possible to a limited extent, because due to external circumstances many attributes of the data can change in the respective department and not all changes are documented. Incompleteness in the dataset - that too will be known to analysts.
Now I asked myself the question: how can I secure my knowledge nevertheless. The nature of the correlation was of central importance.
The situation was similar to a well-insulated building in which the room temperature is dependent on both the outside temperature and a heating. Due to the thick insulation of the building, the outside temperature has a time delay of about two days. After these two days, the temperature in the building has dropped so low that the heater will switch on and heat up the interior of the building. In this example, it quickly becomes apparent that this control loop applies only in winter. In the summer one has to do with a heating of the interior with the same time delay of two days. In winter, there is the additional problem that the heating eliminates the correlation between outside and inside temperature.
Now imagine that the heating of the building is under-dimensioned, and it can not keep the interior of the building to temperature, so that the correlation between outside and inside temperature is maintained.
 |
| Correlation between tboth temperatures with variable time offset (x axis) |
And now we find exactly this correlation - but we do not yet know that the heating is too weak. In general, one would doubt the causality of the correlation, since the building is heated. And that was just the sticking point. So how do you protect the knowledge against "random" correlation? There is no general solution to such problems. But especially for this problem, a solution came to my mind.
What I did not know at the beginning of the investigation was the time span between the Delayed Temperature inside and the outside temperature. So I had to link my data with different time intervals. So I connected the data set of the outside temperature over the date with + X days with the data of the interior temperature and determined the correlation. This was laborious and brought me a series of readings that resembled a curve.
The temperature is constantly changing throughout the year - it is the seasonal element in general. With a time lag of 6 months, the outside temperature reaches its maximum or minimum. After reaching its maximum, the temperature gradually drops after June. After reaching their minimum, the temperature gradually rises after December. At 6 months (ie about 180 days), the correlation of the outside temperature with itself would have to be close to -1 because the behavior of the same magnitude reverses. At three months (about 90 days), the correlation would have to be at zero. The same applies to the interior temperature and +2 days more. Conversely, this would also mean that a curve symmetry would have to be present if the time was shifted in the other direction. So this now had to be tested. I now performed the same elaborate data transformation in the other direction and obtained the following curve of correlation measurements.
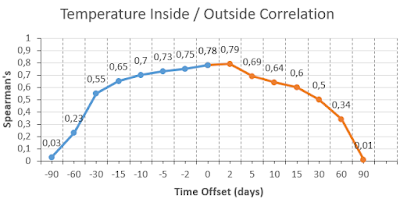 |
| Correlation between tboth temperatures with variable time offset (x axis) from -90 to +90 days |
So the calculated curve about Spearman's correlation coefficient was actually symmetric, and this suggested that it was not a random correlation but a causal one. In a random correlation, it would be extremely unlikely that the result would follow a curve - let alone a symmetric one. The following graphic illustrates what a random correlation would look like.
 |
| Random correlation coefficients across 180 days would show spikes like these |
Kommentare
Kommentar veröffentlichen